Écrire un entier naturel⚓︎
Base binaire⚓︎
On a vu dans l'activité qu'étant donné une base , on peut représenter n'importe quel entier comme la somme de puissances de multipliées par des entiers inférieurs à .
- Base de représentation
-
La base de représentation est la valeur choisie pour décomposer un nombre lors de son écriture.
L'écriture en base d'un nombre sera uniquement composée de chiffres inférieurs à .
Ainsi, si 1534 est écrit en base 10 ce nombre correspond à la valeur . Par contre, si 1534 est écrit en base 8, ce nombre correspond à la valeur .
Par convention, pour dire qu'un nombre est écrit dans la base on écrira : 1534b, ainsi : 153410 désigne la quantité 1534 mais 15348 représente 860.
En informatique, tout les nombres sont représentés en binaire (base 2).
- Bit
- Un bit (binary digit) est un chiffre qui peut valoir 0 ou 1, c'est l'unité fondamentale de mesure de l'information.
- Octet
- Un octet est une suite de 8 bits, on travaillera le plus souvent avec des valeurs encodées sur des octets entiers.
Exemples à faire
Quel est la valeur de : 10110 ? 1014 ? 1012 ? Est ce que 100010119 est une valeur correcte en binaire ? Combien y a a-t-il de bits dans ce nombre : 1001 0011 1111 01112 ? D'octets ?
En python, on a accès à la représentation binaire et aux conversions via quelques fonctions:
0b1010 # Le nombre représenté par 1010 en binaire
0b... # permet d'écrire un nombre en binaire directement
int("10234",6) # donne la valeur de 10234 en base 6
int(suite_chiffre,b) # donne la valeur de la suite de chiffre dans la base b
bin(n) # donne la représentation binaire de n
Du binaire au décimal⚓︎
Les 10 premiers chiffres binaires sont :
| Décimal | Binaire |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
Que remarque t on sur l'écriture des entiers pairs ? Impairs ?
Les entiers pairs s'écrivent avec un 0 comme dernier chiffre. Les entiers impairs eux, s'écrivent avec un 1 comme dernier chiffre
Quels sont les nombres s'écrivant comme un 1 suivi par des 0 en base 2 ? Et en base 10 ?
Les puissances de 2 : En base 10, ce sont les puissances de 10 : 110,1010,10010,100010
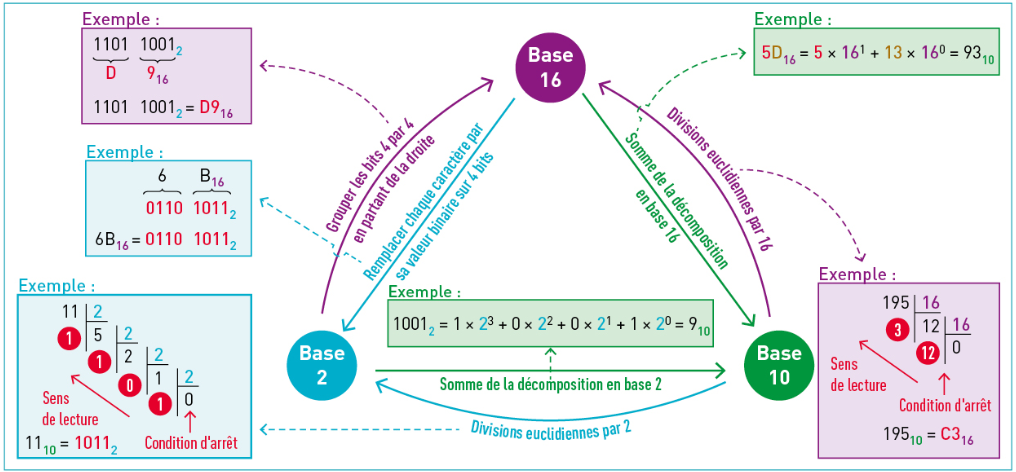
Base hexadécimale⚓︎
La base hexadécimale ou base 16 est la deuxième base la plus utilisée en informatique. On la retrouve sur le web pour représenter les couleurs, ainsi que dans la programmation système ou bas niveau.
Elle permet de facilement représenter de grands nombres binaires, avec peu de chiffres.
- Base hexadécimale
-
La base 16 utilise 16 chiffres, comme les chiffres décimaux ne vont que jusqu'à 9, on leur ajoute les lettres:
A,B,C,D,E,F, qui vont représenter les valeurs de 10 à 15.On peut écrire les lettres en majuscules ou minuscules, sans distinction.
Convertissez les nombres 916, D16 et 1116 en décimal
On a un lien très simple entre la base 2 et la base 16, du au fait que .
Écrivez les nombre 9F16, 916 et F16 en binaire.
Le nombre 9F16 s'écrit comme les nombres 916 et F16 collés en binaire. Soit : 916 = 10012, F16 = 11112, 9F16 = 1001 11112. Il prend 8 bits, donc 1 octet.
On peut donc remarquer qu'un nombre hexadécimal s'écrit sur un octet, mais est-ce toujours le cas ?
Faites de même pour 5216 ? À quoi faut il faire attention ?
5216 s'écrit : 0101 00102 On doit bien ajouter des 0 pour faire 4 bits pour chaque chiffre hexadécimal
- Conversion binaire depuis hexadécimal:
- Pour convertir un nombre hexadécimal en binaire, il suffit d'écrire chaque chiffre hexadécimal sur 4 bits, dans l'ordre. On peut faire cela car , c'est une base puissance de la base binaire.
La correspondance entre les trois bases est la suivante:
| Décimal | Binaire | Hexadécimal |
|---|---|---|
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
Écrivez 6616, 5F16 et 1116 en binaire.
- 6616 s'écrit: 0110 0110
- 5F16 s'écrit: 0101 1111
- 1116 s'écrit: 0001 0001
Devoir ?
Sans calculer leur valeur décimale, comment écrire les nombres suivants en hexadécimal:
- 11112 =
- 10002 =
- 1111 10002 =
- 1010 01102 =
- 1110 0111 11002 =
- Conversion binaire vers hexadécimal:
- Pour convertir un nombre en binaire vers de l'hexadécimal, on groupe ses bits par 4 en partant de la droite, puis on convertit chaque groupe de 4 bits en un chiffre hexadécimal.
De même que pour le binaire, l'hexadécimal est assez répandu pour avoir ses propres écritures en python:
0x5D # Le nombre représenté par 5D en hexadécimal
0x5d # Le même nombre
0x... # permet d'écrire un nombre en hexadécimal directement
int("ABC1E",16) # donne la valeur de ABC1E en base 16
hex(n) # donne la représentation hexadécimale de la valeur n
Devoir ?
Dans la fiche suivante, faites les exercices 2,4,5.1 et 6.
Base décimale⚓︎
On a l'habitude d'écrire nos nombres en base 10. Pour passer à l'écriture dans une autre base on peut utiliser l'algorithme des divisions successives:
- Algorithme des divisions successives:
-
Pour décomposer un entier dans une base, on le divise par la base jusqu’à avoir un quotient nul. La suite des restes obtenus est alors la représentation du nombre dans la base donnée. On effectue donc l'algorithme suivant:
- Soit le nombre dont on veut la représentation dans la base .
- On calcule le quotient et le reste dans la division entière de par soit : avec
- On recommence avec , tant que n'est pas nul.
- La suite des restes obtenus est alors la représentation de dans la base .
Représentation de 25 en base 2
| Division | Représentation | |
|---|---|---|
| devient 12 | "...1" | |
| devient 6 | "...01" | |
| devient 3 | "...001" | |
| devient 1 | "...1001" | |
| devient 0 | "...11001" |
est nul, donc on s'arrête. Donc 2510 s'écrit 110012, on peut l'écrire sur un octet comme : 0001 10012
- Algorithme des soustractions successives:
-
Pour décomposer un entier dans une base, on lui soustrait la plus grande puissance de deux possible. Si on peut soustraire , alors on écrit un 1 à la -ième position, puis on recommence avec la différence obtenue.
On effectue donc l'algorithme suivant:
- Soit le nombre dont on veut la représentation dans la base .
-
On trouve le plus grand tel que
-
On le soustrait à et on recommence avec le nouveau nombre
- La suite des nombres soustraits donne les coefficients de la décomposition en base 2.
Représentation de 25 en base 2:
| Puissance inférieure | Représentation | |
|---|---|---|
| et | devient | |
| et | devient | |
| et | devient |
est nul, donc on s'arrête. Donc 2510 s'écrit , on peut l'écrire sur un octet comme : 0001 10012
Utilisez ces algorithmes pour calculer la représentation de 13 et 38 en base 2
On applique notre algorithme:
.
.
.
Donc
.
.
Donc
Taille d'entiers⚓︎
Un octet ne permet pas de stocker tout les nombres possibles, seulement les nombres de 0 à 255. Lorsque l'on cherche à stocker un nombre qui ne rentre pas dans un octet, on a un phénomène dit d'overflow, de l'information est perdue.
Pour remédier ce phénomène, on utilise plusieurs octets pour stocker les entiers. La question est alors: Combien faut il de bits (d'octets) pour représenter un entier donné ?
Questions⚓︎
Quels entiers peut on écrire avec 4 bits ? 8 bits ?
Avec 4 bits, on peut écrire les entiers de 00002 à 11112 soit 010 à 1510. Avec 8 bits, on peut écrire les entiers de 0016 à FF16 soit 010 à 25510
- Encadrer la taille d'un entier, sans calculer sa représentation
-
Pour un entier donné, il faut autant de bits pour le stocker, que pour stocker la plus petite puissance de 2 immédiatement supérieure.
Ainsi, pour évaluer la taille en binaire de 57, on doit trouver tel que . Pour 57, on sait que soit , donc il faudra 6 bits pour représenter 57.
Combien faut il de bits pour représenter 110 ? 710 ? 1510 ?102310 ?
1,3,4,10
Complétez ceci pour 1,3, octets
| Nombre d'octets | Nombre de bits | Nombre d'entiers stockables | Maximum |
|---|---|---|---|
| 1 | 8 | ||
| 3 | |||
| n |
Pour chaque intervalle, on peut stocker un nombre minimum (0) et un nombre maximum, qui correspond à mettre tout les bits à 1.
- Nombres binaire de la forme : 1111...
-
Le plus grand nombre binaire représentable sur bits est celui où les bits sont à 1.
Ce nombre vaut Pourquoi ?
- Extremums:
- Avec bits, on peut stocker les nombres de 0 à On peut donc stocker nombres sur bits.
Problème: Si on additionne deux entiers, combien faut il de bits pour stocker le résultat ?
Pour répondre, essayons sur deux entiers : 3 et 2 puis 8 et 6, écrivez les en binaires, puis leur somme en binaire
et pour 8 et 6
Ici, additionner deux entiers de taille 2 crée un entier de taille 3, mais additionner un entier de taille 4 et un de taille 3 donne un entier de taille 4.
- Taille de la somme:
-
Soit deux entiers encodés en binaire, de même taille .
Leur somme demandera au maximum bits pour être stockée.
Démonstration
Le plus grand nombre codable sur bits est . La plus grande somme possible de nombres sur bits est donc
.
comme , il faut bits pour le stocker.
De la même manière, on peut calculer la taille maximale du produit de deux entiers codés sur bits.
- Taille du produit:
-
Soit deux entiers encodés en binaire, de même taille .
Leur somme demandera au maximum bits pour être stockée.
Démonstration
Le plus grand nombre codable sur bits est . Le plus grand produit possible de nombres sur bits est donc
or il faut donc bits pour le stocker au maximum.
Opérations sur les entiers⚓︎
Ici on décrit les opérations en base 2 et 10, mais la même logique s'applique pour la base 16. Il vous suffit de mettre la retenue quand la somme est supérieure ou égale à 16 et non à 10 ou 2.
Addition⚓︎
On sait poser une addition en base 10 avec des retenues.
1 5
+ 1 9 8
--------
2 1 3
Pour poser une addition en binaire on exécute exactement les mêmes opérations, sauf que la retenue arrive dès que l'on dépasse 1
Multiplication⚓︎
Pour la multiplication, on peut aussi la poser comme en base 10 et les retenues sont effectuées de la même façon.
1 1 = 3
* 1 0 1 = 5
-------
1 1 = 3
+ 0 0 0 = + 0
+ 1 1 0 0 = + 12
---------
1 1 1 1 = 15 = 3 * 5
Le décalage⚓︎
On a remarqué que les entiers 100... sont toutes les puissances de 2, on va maintenant observer l'opération qui consiste à ajouter des 0 devant un nombre binaire.
Comment passer de 1110 à 110010 ? de 2310 à 230010 ?
On ajoute 2 zéros à droite, ce qui correspond à multiplier par 100.
Si ajouter 4 zéros multiplie par , que fait on quand on ajoute 5 zéros ? 8 zéros ? zéros ?
Comme en base 10, cela permet de multiplier par .
- Décalage de bits:
- Lorsqu'on ajoute zéros à droite d'un nombre écrit en binaire, on le multiplie par . En règle générale, ajouter zéros à droit d'un nombre écrit en base le multiplie par . C'est pour cela que les nombres de la forme correspondent aux puissances de .